|
|
Post by Duvidoso on Feb 24, 2015 16:14:43 GMT -3
Não consigo prosseguir com o que ele pede na questão 17 e nem por que foi necessário usar o 15 no 16 (parte final), sendo q da pra fazer diretamente. Bom eu sei qual o desenvolvimento de $ s/(1+s^2)^{1/2} $ mas de que forma isso vai fornecer $J_{0}$? Tentei usar algo parecido com uma igualdade de séries só que em uma delas o que aparece são termos que envolvem $(1/s)^{k}$ o que fica meio inviável fazer a igualdade, a não ser que eu tenha que eu novamente expanda cada um desses $(1/s)^{k}$ isso seria inviavel? Obs: ele ainda não falou sobre o uso de serie de potência pra resolução de EDO ate ai, e apesar de já ter visto o caso geral desse tipo de função gostaria de entender como seria o andamento q ele pede na 17 o foco é esta questão mesmo. imageshack.com/i/pc1Os4ajj |
|
|
|
Post by Thiago Nascimento on Feb 24, 2015 22:55:55 GMT -3
Aquele $ \mathscr{L} $ é Transformada de Laplace? Pelo que estou vendo, se você fizer o que ele pede, você terá a Transformada de $J_0$ em série de potências, e não $J_0$.
Alguém sabe como faz aquele L estilizado ali?
|
|
|
|
Post by Duvidoso on Feb 24, 2015 23:20:48 GMT -3
Aquele $ \mathcal{L} $ é Transformada de Laplace? Pelo que estou vendo, se você fizer o que ele pede, você terá a Transformada de $J_0$ em série de potências, e não $J_0$. Isso mesmo, por isso não consegui encaixar nada. Existe um argumento que não consigo ver, a partir daí, eu sei que $s.\mathscr{L}[f]-1=\mathscr{L}[f"]$ mas mesmo assim fica faltando algum argumento pra calcular a inversa. E se possível algo para uma serie de potência iriamos ter q achar outra serie de potencia a partir dai, pelo menos não vi nenhum método de resolução onde eu andei lendo sobre o assunto. Basta usar \mathscr{L} Vlw Thiago |
|
|
|
Post by Thiago Nascimento on Feb 24, 2015 23:26:13 GMT -3
Estou vendo aqui, se você expandir e aparecer somas do tipo $\frac{c}{s^{n}} $ quando você calcular a Transformada de Laplace inversa você terá $ c*t^{n}$. Ou seja, parece que vai dar uma série de potências. Acho que se você fizer isso vai obter o que o exercício quer.
|
|
|
|
Post by Duvidoso on Feb 24, 2015 23:33:39 GMT -3
Estou vendo aqui, se você expandir e aparecer somas do tipo $\frac{c}{s^{n}} $ quando você calcular a Transformada de Laplace inversa você terá $ c*t^{n}$. Ou seja, parece que vai dar uma série de potências. Acho que se você fizer isso vai obter o que o exercício quer. Eu expandi de varias maneiras, a expansão em serie binomial iria fornecer uma soma infinita termos da forma $C_{-1/2}^{n}.s^{2n+1}$, essa foi a que me pareceu mais convincente, tem uma q aparece como o inverso de uma serie de potência mas essa eu bem quis mexer pq sabia que eu ia voltar pra o que eu já tinha. Vou tentar achar uma serie de potência com essas parcelas. Já tinha pensado em algo parecido mas n consegui uma saída. |
|
|
|
Post by Duvidoso on Feb 25, 2015 18:52:01 GMT -3
Aqui, deu certo.  |
|
|
|
Post by Thiago Nascimento on Feb 25, 2015 23:23:27 GMT -3
Opa, então deu certo. Você encontrou a relação dos exercícios anteriores com esse? No caso o motivo dele ter dado o passo a passo. 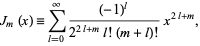 |
|
|
|
Post by Duvidoso on Feb 26, 2015 0:49:31 GMT -3
Opa, então deu certo. Você encontrou a relação dos exercícios anteriores com esse? No caso o motivo dele ter dado o passo a passo. 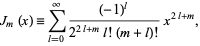 Opa essa dai não é solução da equação de ordem m?, eu entendi o por que dele usar o 15 no 16, também é só pra deixar claro que a constante que aparece depois das integrações vai ser 1, e daí vai ficar só $1/(1+s²)^{1/2}$, ele queria mesmo dar uma introdução sobre o que virá nos próximos capítulos. Valeu, bacana mesmo o legal é que da pra mostrar que vale para todo $m\in\mathbb{R}$. |
|
|
|
Post by Thiago Nascimento on Feb 26, 2015 13:14:16 GMT -3
Sim, a função de Bessel do primeiro tipo de ordem n, é a solução dessa equação diferencial que é não-singular na origem: 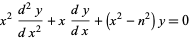 Aí você consegue expandir a solução em séries também e a $ J_m $ em séries fica: 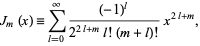 |
|